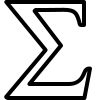Description

📊 Standard Deviation Calculator

🔍 What is a Standard Deviation Calculator?

A Standard Deviation Calculator helps you measure how spread out or dispersed a set of numbers is from the mean (average). It’s a core concept in statistics, probability, and data analysis, useful for understanding data variability. 📈

📈 Why Use Our Standard Deviation Calculator?

✅ Accurate Results – Instantly compute population or sample standard deviation
✅ Step-by-Step – Shows how mean, variance, and deviation are calculated
✅ Flexible – Works with both small data sets and large numbers
✅ Time-Saving – No need for manual formula work
✅ Free & Online – Accessible anytime, anywhere

🏫 Perfect For:

• Students studying statistics & probability 📘

• Teachers explaining data distribution ✏️

• Researchers & Scientists analyzing experiments 🔬

• Financial Analysts measuring market risk 📉

• Data Analysts working with large data sets 💻

📐 Understand Standard Deviation Like a Pro

• Measure data spread around the mean

• Compare sample vs. population deviation

• Analyze consistency and variability in data sets

• Apply results in finance, science, education, and research

📘 Common Questions – Standard Deviation Calculator

Q1. What is standard deviation?
✅ Standard deviation measures how much data values deviate from the mean. A low value means data points are close to the mean, while a high value means greater spread.

Q2. What’s the difference between population and sample standard deviation?
✅ Population SD considers the entire data set, while Sample SD uses a subset of data (with n−1n-1n−1 in the formula to reduce bias).

Q3. Why is standard deviation important?
✅ It helps understand data variability, compare different data sets, and is widely used in finance, quality control, research, and risk management.

Q4. What formulas are used in standard deviation?
✅ For a population:

σ=∑(xi−μ)2Nσ = \sqrt{\frac{\sum (x_i - μ)^2}{N}}σ=N∑(xi​−μ)2​​

For a sample:

s=∑(xi−xˉ)2n−1s = \sqrt{\frac{\sum (x_i - \bar{x})^2}{n-1}}s=n−1∑(xi​−xˉ)2​​

Q5. How does this calculator help in real life?
✅ It simplifies analyzing exam scores, financial returns, survey data, scientific results, and any dataset where consistency and variation matter.

🔗 Explore More Statistics Tools

• Triangle Calculator – Measure variability in data sets

• Z-Score Calculator – Standardize data points